PhD Dissertation

Designing Cryptography Systems for GNSS Data and Ranging Authentication

For anyone who desires to design a PNT system resistant to spoofing attacks with cryptographic methods (or is otherwise interested in the topic).

Dissertation

Defense Presentation Recording

Defense happened on April 9th at Stanford University. Watch below or on YouTube.

Abstract

The GPS has profoundly changed commercial aviation over the last three decades. Today, GPS (and the broader global system, GNSS) pervades our everyday lives, including safety-critical aspects ranging from commercial aviation to electrical grid time synchronization. Autonomous vehicles rely on GNSS signals to estimate vehicle position and time. GNSS’s open nature and ubiquitous adoption lend a potentially fatal vulnerability. Anyone can broadcast spoof signals to fool a receiver into believing GNSS is safe when, in fact, it is hazardous, thus perpetually casting doubt on GNSS accuracy. Spoofed GNSS signals are an undeniable reality of modern conflict zones and are likely to spread worldwide. What started as fooling Pokemon Go can now affect the safety-critical aspects of our lives. This dissertation explores augmenting GNSS signals with cryptographic methods to establish trust in the signals.

A GNSS engineer can use this dissertation to inform the system and receiver design to mitigate spoofing risks using cryptography. From a GNSS provider perspective, this dissertation covers the elements of cryptographic construction for provable security, efficient bandwidth use, and quick authentication time. The primary authentication structure a GNSS Provider should use is TESLA. This dissertation describes leveraging TESLA’s features, designing the needed security maintenance structures with standard asymmetric authentication cryptography, and asserting the TESLA time-synchronization requirements. Moreover, TESLA enables ranging authentication via ranging code watermarking without additional data-distribution bandwidth. This dissertation describes how to securely perform watermarking in a way that allows straightforward derivation of the distribution of receiver-measured statistics. From a GNSS receiver perspective, this dissertation covers the receiver processing required to establish trust in the GNSS signal, including computing the security they afford.

Previously, the severely constrained GNSS data bandwidth posed significant challenges to incorporating cryptography, often dictating the product (i.e., the service the GNSS constellation could offer). However, a significant shift occurs with the techniques presented in this dissertation. Whereas before, cryptography dictated the product, the product can now dictate the cryptography.

GNSS Authentication Background

The GNSS signals contain two components: (1) the data component and (2) the ranging component. The data distributes information about the positions of the satellites. The ranging component allows receivers to deduce their range to the satellite. With four satellites, a receiver can use the data and ranging components to deduce its position and time. Both the data and the ranging components can each be augmented with cryptographic methods.

Data Authentication

GNSS signals broadcast various information regarding each satellite’s orbits and status. For instance, WAAS will notify commercial aircraft flying in the USA that GPS is malfunctioning within 6 seconds of detecting a GPS anomaly. To protect against spoofing, GNSS could add the internet cryptography we use every day; however, utilizing authentication cryptography out of the box poses challenges.

The principal challenge of GNSS Data Authentication is the limited data bandwidth. The GPS data connection is 50 bits per second, compared to a single ECDSA digital signature requiring around 512 bits. Concretely, imagine needing 20 seconds to broadcast an authentication signature for a 1-second message. To accommodate this concern, a specialized cryptographic authentication protocol called Timed Efficient Stream Loss-tolerant Authentication (TESLA) is needed.

TESLA is a delay-released bit-commitment scheme that provides several efficiency advantages. GNSS will want to construct an authentication scheme like the one below to maximize the data bandwidth efficiency.

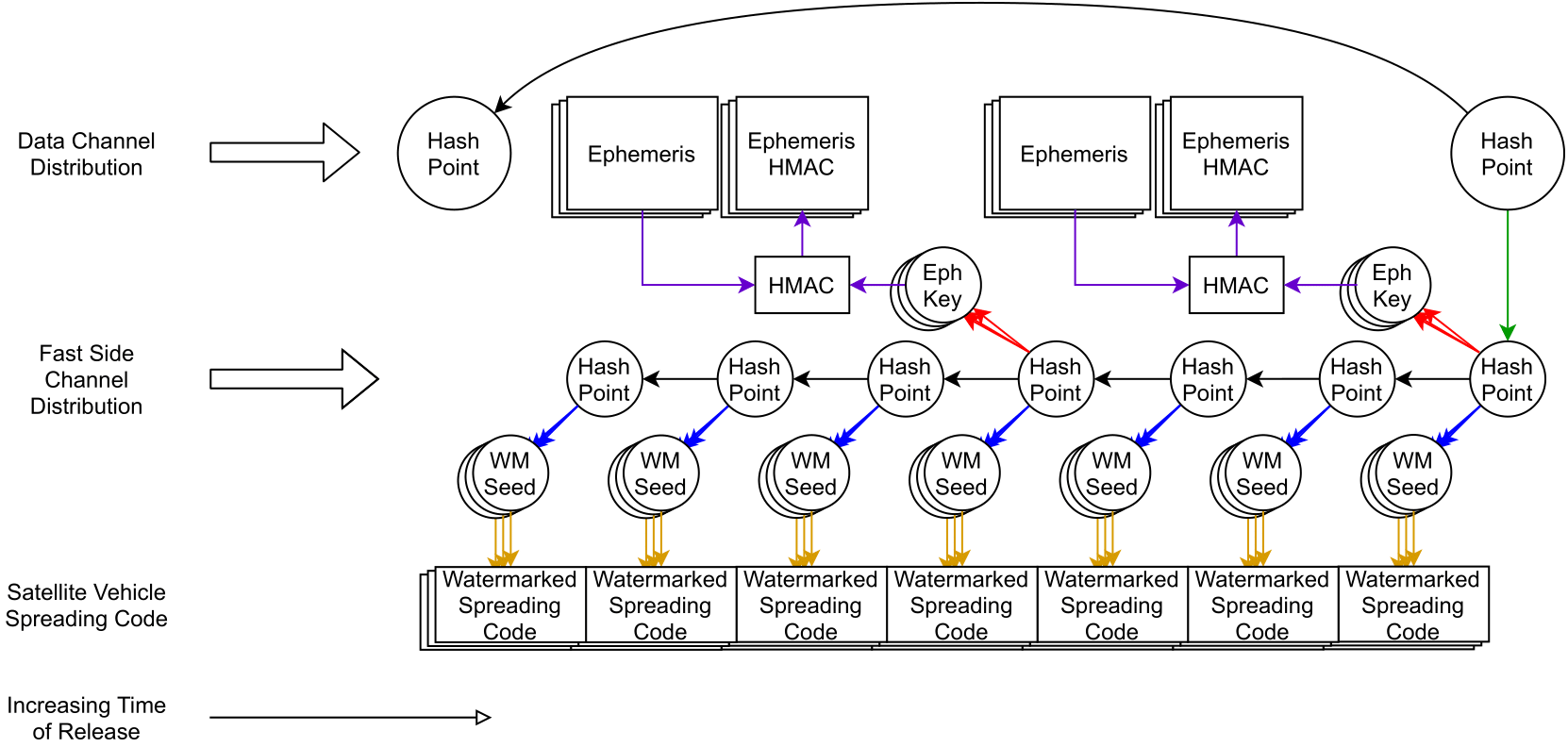
The diagram reads from left to right, with GNSS increasing broadcast time. Each circle represents a cryptographically derived seed, with each arrow representing a one-way cryptographic hashing operation. In my work, I refer to the cryptographic TESLA distributions as Hash Points, referring to the branching geometry that enables highly efficient cryptography (sparing us yet another use of cryptographic key*). The top row represents the data channel used by the no-internet receiver. The second row of Hash Points enables faster, internet-based authentication without conflicting with the data channel’s non-internet distributions. Further branching enables all satellites to be cross-authenticated (decreasing the time to authentication by an order of magnitude) and ranging authentication techniques without additional data bandwidth (see next section). In the following articles, I detail how to exploit TESLA’s bandwidth efficiency features for GNSS authentication.

Publications Regarding Efficient Cryptography Structures for GNSS
Cryptographic Ranging Authentication with TESLA, Rapid Re-keying, and a PRF
Efficient and Secure Use of Cryptography for Watermarked Signal Authentication

Ranging Authentication

GNSS signals broadcast a repeating 1023-bit pseudorandom signal called a Gold code. The receiver correlates a local replica of the Gold code with the received radio signal. The peak of the correlation allows the receiver to measure the signal transit time from satellite to receiver (and with 4 satellites, the receiver can deduce its position).

In my work, one of the concepts I investigate is an authentication technique called watermarking. With watermarking, the Gold code is secretly pseudorandomly perturbed (but not so perturbed as to materially disrupt existing GNSS receivers). The perturbation decreases the correlation peak. Later, the perturbation is revealed to the GNSS receiver. If the receiver observes an increase in the correlation after re-correlating with the distributed perturbation, it has evidence of the signal’s authenticity.

In my work, one of the contributions includes deriving the distribution of this difference statistic when using Combinatorial Watermarking. Using my derivation, one can design a signal and make claims about the probability a spoofer could fool a receiver using watermarks to authenticate the signal. You can read more about this in the following publications (and several soon to be published not yet listed).

Publication for Deriving the Distribution of the Correlation Difference
Authentication Security of Combinatorial Watermarking for GNSS Signal Authentication
Combinatorial Watermarking for GNSS Signal Authentication

Time Synchronization, Rekeying, etc

More information on these topics can be found here.